三平方の定理(ピタゴラスの定理)の例題や計算のやり方、証明、応用・難問などのまとめはこちらです 「三平方(さんへいほう)の定理」は、 中学数学で最後に出てくるけど、1番大事な定理の1つです。 高校入試では、複雑な図形の問題が出題されますが、 直角を探したり、 補助線をうまく引くことで直角を作ったりして、 三平方の定理を使える形にする$0< a,b,c < 100$ の範囲のピタゴラス数を探すプログラムを作成し、その範囲のピタゴラス数を全て列挙してみなさい。 ヒント $n>2$の場合には$a^n = b^n c^n$を満たす整数の組 a,b,c は存在しない、という有名な フェルマーの定理 がワイルズによって証明されたのは(数学の歴史上は)つい最近の中学生 数学 3年 三平方の定理 ピタゴラスの定理 練習問題 答えと解答はこちら。 高校入試 では 三平方の定理 を使った問題は必ず出ます。 (出ると思います。 ) 定期テストで平均点レベル、あるいは平均点以下の中学生は、この問題を確実に正解できるようにしてください。 (1)まず、その問題が、どの項目からの出題か考える。 見たことのない文章問題で
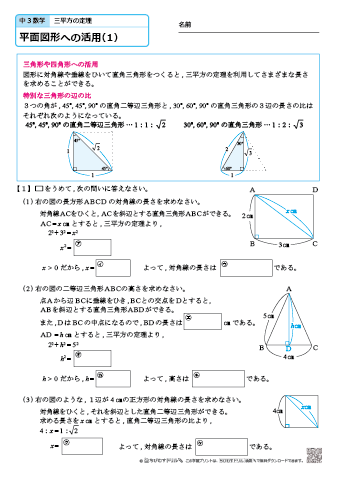
中学3年生 数学 三平方の定理 平面図形への活用 練習問題プリント ちびむすドリル 中学生
ピタゴラスの定理問題集
ピタゴラスの定理問題集- 逆ピタゴラスの定理(符号問題)⚠️ 3 ツイート宇宙の星屑板 年10月27日 2121 「逆ピタゴラスの定理(符号問題)⚠️」 👽:(2/3)(1/3)=3/3 01×03×(10)=30「ユークリッド原論」の「三平方の定理」は始めから「ピタゴラスの定理」 と呼ばれたわけではありません。このように呼ばれるようになったのは 「ユークリッド原論」が書かれてから数世紀が経過してからです。 プロクロス (Proclus, 412~485) は




コラム ピタゴラスの定理 江戸の数学
三平方の定理の練習問題10問・解き方の解説 管理人 5月 27, 三平方の定理に関する問題は様々なパターンのものが出題されます。 初見では難しい問題が多いのですが、大体はパターンが決まっているので、ひとつずつポイントを抑えて問題に慣れてここではこのピタゴラスの定理が人間の知恵の象徴として使われています。 問題1 上の2つの正方形を図のように分割します。 これを並び替えると、下の大きな正方形を作ることができます。 このことでピタゴラスの定理を証明してください。 DFの長さをxcmとして、三平方の定理(ピタゴラスの定理)に代入してみると、 13² = 5² x² x = 12 あら不思議! 長さがわからない直角三角形の辺を求めることができたね。 >>三平方の定理(ピタゴラスの定理)の計算問題にチャレンジ!
逆ピタゴラスの定理を使えば, 命題1 を図形的に示すことができます。 まず,斜辺を ,残りの2辺を , となる直角三角形を用意します( , , はピタゴラス数)。このとき,斜辺からの三角形の高さを とすると,逆ピタゴラスの定理より ,すなわち と三平方の定理(ピタゴラスの定理): \angle C=90^ {\circ} ∠C = 90∘ であるような直角三角形において, a^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。ピタゴラス数とは,直角三角形の3辺の長さとなるような3つの整数の組のことです。 ピタゴラスの定理(三平方の定理)を使うと, a 2 b 2 = c 2 a^2b^2=c^2 a 2 b 2 = c 2 を満たす自然数の組 (a, b, c) (a,b,c) (a, b, c) をピタゴラス数と呼ぶ。 と言うこともできます。 例えば,
対象商品 数学100の定理―ピタゴラスの定理から現代数学まで 数学セミナー編集部 単行本 ¥2,750 残り2点(入荷予定あり) この商品は、Amazoncojpが販売および発送します。 通常配送無料(一部の商品・注文方法等を除く) 詳細 数学100の問題―数学史を 問題解決のポイント 今回のピタゴラスの定理は、ピタゴラス数を求めるアルゴリズムの問題です。 恐らく競技プログラミングをやられている方などは馴染みがあるのではないでしょうか。 (私は分かりませんでした。。。) ピタゴラス数を全て求める公式として以下の値が用意されていま直角三角形の3辺の長さに関する a 2 b 2 =c 2 という関係は ピタゴラスの定理 (三平方の定理)と呼ばれます。 この定理はその名の通り古くから知られていますが、本当にピタゴラス (cBC570cBC500)が発見したかどうか確証があるわけではありません。 ピタゴラスの定理 3世紀にディオゲネス・ラエルティオスは『哲学者列伝』の中で「算数家のアポロドロスによれば
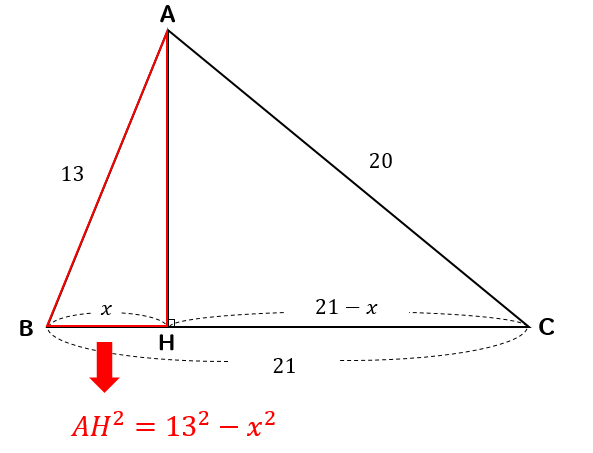



三平方の定理 方程式を利用する発展問題を解説 数スタ
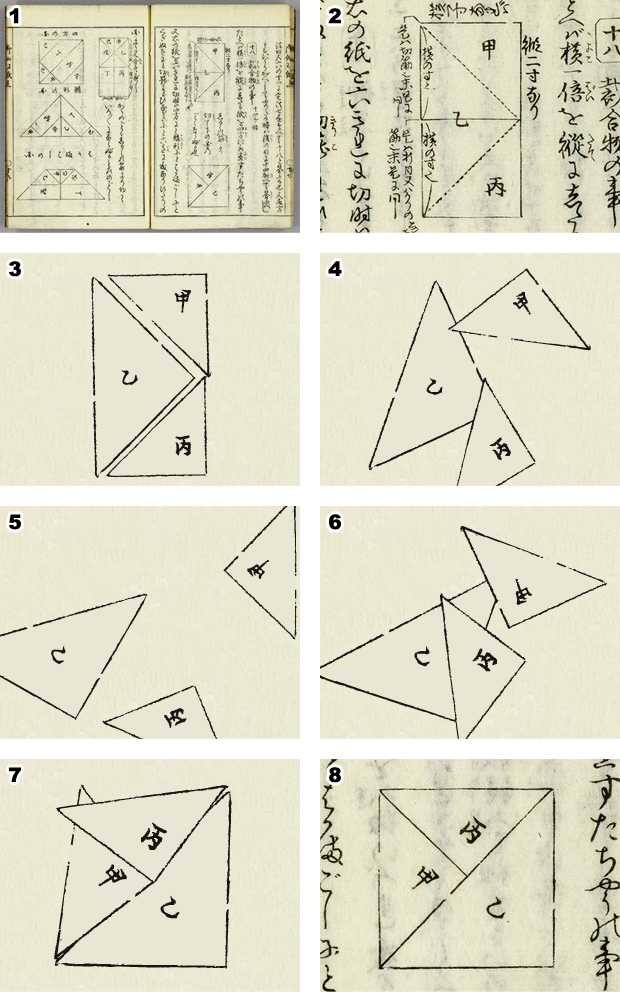



コラム ピタゴラスの定理 江戸の数学
「ピタゴラスの定理(三平方の定理)」の(やや)トリッキーな証明を紹介します。 About Press Copyright Contact us Creators Advertise Developers Terms Privacy発展問題:最初に考えた問題は、同じように縄を使って解けるでしょうか? <ピタゴラス数・三平方の定理が発見された地域> 中国 句股定理 ギリシア ピタゴラスの定理 エジプト (3,4,5) の ピタゴラスAmazonで白鳥 敬, あきら, すぎうらの定理と法則101―ピタゴラス、フェルマー、アインシュタインから現代まで (大人の「科学」と「学習」)。アマゾンならポイント還元本が多数。白鳥 敬, あきら, すぎうら作品ほか、お急ぎ便対象商品は当日お届けも可能。




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ




三平方の定理の応用問題 中学3年数学 Youtube
おなじみの問題。 全て円弧です。 A 約31.5c㎡ 100π/3 正方形が三つ並んでいます。 実は、ピタゴラスの定理を使わなくても簡単に求められます。 A 45° 簡単にできると思って取り組んだら、けっこう難しかった問題。 ピタゴラスの定理 大矢真一著 参考 下の図1は、直角三角形ABCの4倍とc²とで一つの正方形を作っている。 それを図2のように、直角三角形を動かすと、直角三角形四つとおよびで同じ正方形になる。 それゆえととは等しくなる。 これを代数的に考えると、 大きな正方形の一辺は、である。 直角三角形の面積はである。 よって図1において c²+2ab=(a+b)²6.実際の問題への応用 その1 (1) ピタゴラスの定理より AC=10cm 対角線3等分の定理より AR= cm 2 対角線3等分の定理より 2 (3) 五角形PBQSR=長方形- APD- DQC- DRS =48-12-12-8=16cm 2 ※この定理を知らなければ・・・・ちょっと大変かも。(@_@) その2




コラム ピタゴラスの定理 江戸の数学
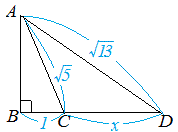



三平方の定理の応用
三平方の定理(ピタゴラスの定理)の応用問題パターン10選 三平方の定理(ピタゴラスの定理)は、直角三角形において成り立つ定理です。 また、どんな定理だったかと言うと、$3$ 辺の長さについてピタゴラスの定理の証明を集めた本は多数あるが,今回の記事を書くにあたり,『ピタゴラスの定理 $100$ の証明法 ― 幾何の散歩道』(森下四郎著,プレアデス出版)を参考にした.証明が種類別に分けられ,系統的に説明されていて分かりやすい.考えて ^大矢, 真一『ピタゴラスの定理』東海大学出版会〈Tokai library〉、01年8月。ISBN 。 ^ 大矢, 真一『ピタゴラスの定理』東海大学出版会〈東海科学選書〉、1975年。 ^ 大矢, 真一『ピタゴラスの定理』東海書房、1952年。 ^ 亀井喜久男 "エジプトひもで古代文明に挑戦し




中学3年生 数学 三平方の定理 平面図形への活用 練習問題プリント ちびむすドリル 中学生
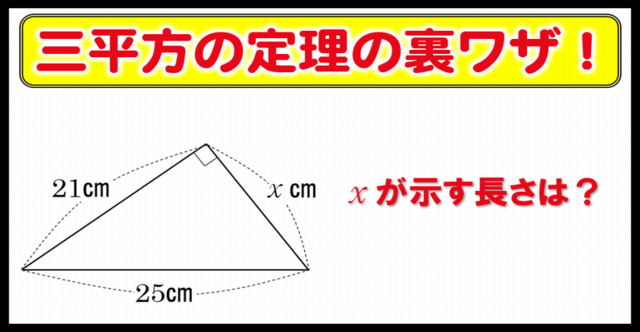



5秒以内に解けますか 賢く解きたい三平方の定理の裏ワザ 暇つぶしに動画で脳トレ
ピタゴラス3体問題とは 昔の人は思った、特別な位置に3つの天体があればそれは規則的、もしくは美しい軌道を描くのではないか、と。 それが着想だったに違いない。そしてピタゴラスの定理。 3, 4, 5、この3つの数字は $$ 3^2 4^2 = 5^2 $$ という等式で結ば残り 1 辺を三平方の定理を使って求めると、 三平方の定理 1 2 x 2 = 2 2 これを解いて、 x = 3 よって、その辺の比は、 1 2 3 となります。 ② 45 °, 45 °, 90 ° POINT:正方形の半分 正方形の 1 辺の長さを①とすると、 1 辺は同じ長さなので①となります初等幾何学 における ピタゴラスの定理 (ピタゴラスのていり、 英 Pythagorean theorem )は、 直角三角形 の3 辺 の長さの関係を表す。 斜辺 の長さを c, 他の2辺の長さを a, b とすると、定理は c 2 = a 2 b 2 {\displaystyle c^ {2}=a^ {2}b^ {2}} が成り立つという 等式 の形で述べられる 。 三平方の定理 (さんへいほうのていり)、 勾股弦の定理 (こうこげんのていり)とも呼ば



しょうちゃん 公式ブログ 算数の問題を解いてみる その84 ピタゴラスの定理 円の性質 Powered By Line
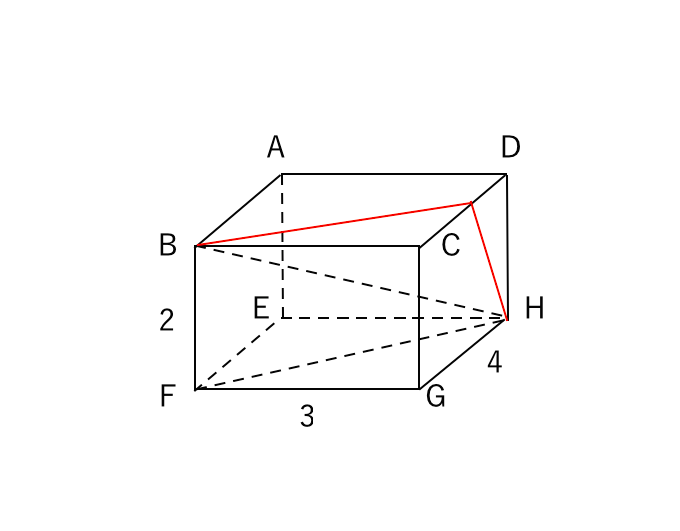



三平方の定理 立体 苦手な数学を簡単に
a 2 b 2 = c 2 ⇒ ( a t) 2 ( b t) 2 = ( c t) 2 つまり,ピタゴラス数がひとつみつかったら,その自然数倍は必ずピタゴラス数です. a, b, c a, b, c が互いに素であるようなピタゴラス数は 原始ピタゴラス数 と呼びます.たとえば, (3, 4, 5), (8, 15, 17) ( 3, 4, 5), ( 8, 15, 17) などは原始ピタゴラス数です.また, (9, 12, 15), (10, 24, 26) ( 9, 12, 15), ( 10, 24, 26) などはピタゴラス数では ピタゴラスの定理 ピタゴラスの定理の証明 この定理には数百通りもの異なる証明があり、例えば、「以下では頂点 a, b, c からなる三角形を abc と表す」「各辺 ab, bc, ca に向かい合う角を ピタゴラスの定理・三角関数・ルート計算方法 数学ノート 大学受験の次男から、この問題、教えてくれと言われ、全く分からなかったのが以下の問題です。 『三角形でA角が45度、B角が75度、C角が60度で、BCの長さが√6のとき、ACの長さを求めよ』 この



Studydoctor三平方の定理の応用問題 中学3年数学 Studydoctor




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
ピタゴラスの定理の導入マスタープラン Designed by S Yamamoto, 授業コンセプト 対象学年:中学校3年生 このマスタープランは,「三平方の定理」の単元(中 学校3年生)の第1時間目の授業のためのプランで直角二等辺三角形befの面積は?(06年算数オリンピック、ファイナル問題より)() 色のついた部分の面積合計は?(大阪星光学院中学 12年)() 三平方の定理、小学生バージョンの解き方(江戸川女子中 09年)()



最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ




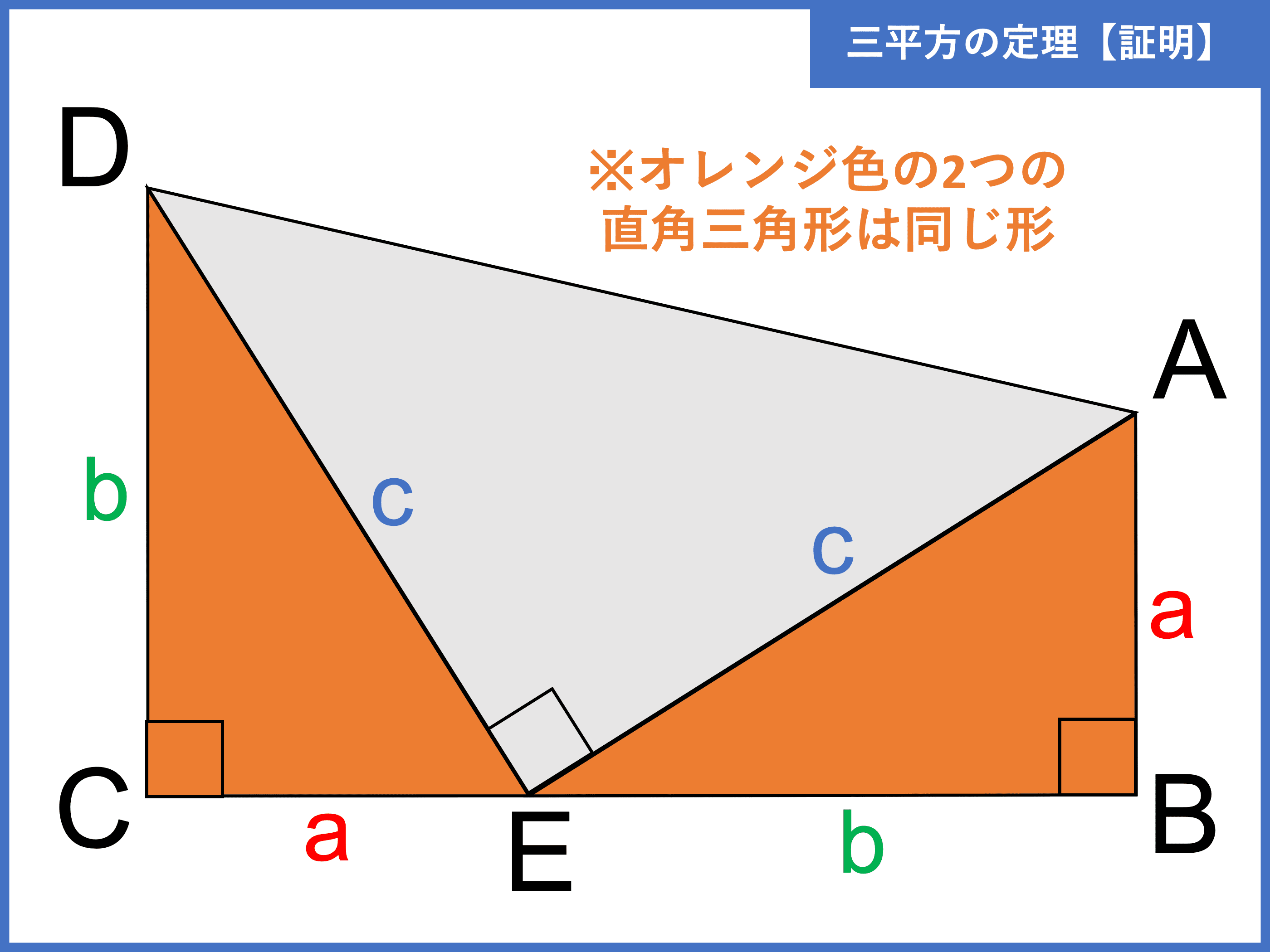
三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも
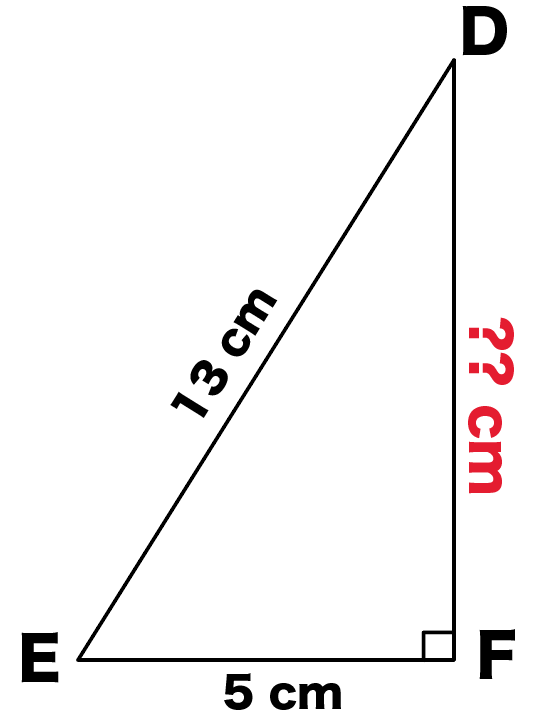



3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



三平方の定理
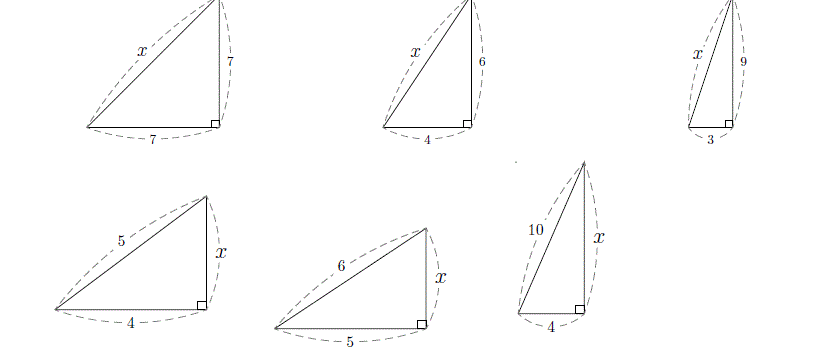



かみのドリル 三平方の定理



三平方の定理




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




Mathematics 三平方の定理 3 いろいろな三角形 働きアリ



三平方の定理




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




世界一わかりやすい数学問題集中3 7章 三平方の定理
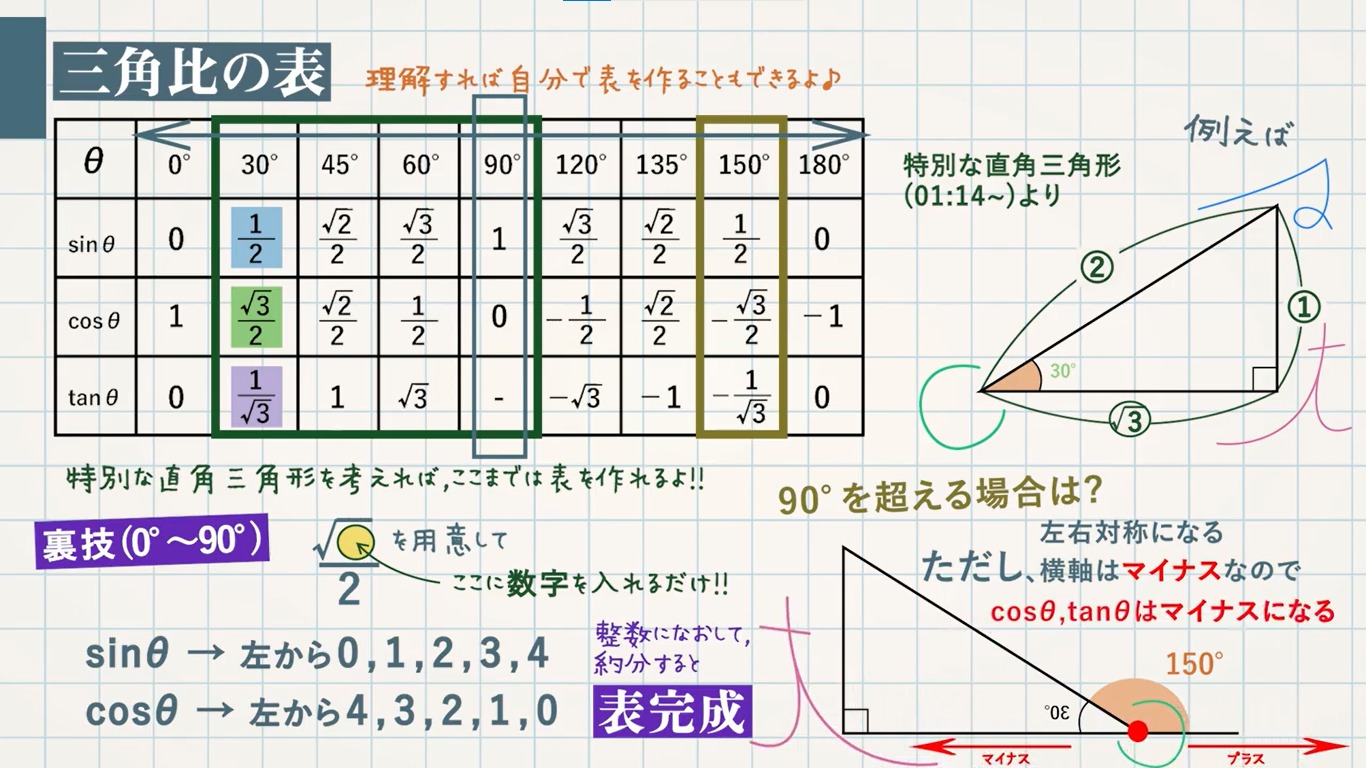



三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト




中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット



Studydoctor三平方の定理と四角形への利用 中学3年数学 Studydoctor




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube




三平方の定理 平面図形のいろいろな応用問題 無料で使える中学学習プリント




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
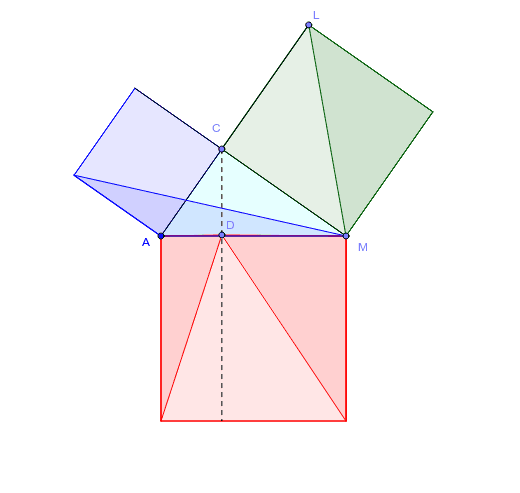



ピタゴラスの定理 ユークリッドの証明 Geogebra
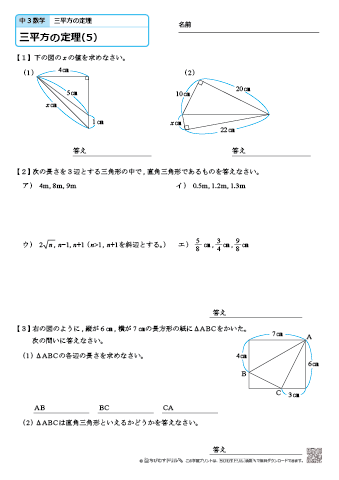



中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



Math 高校入試の難問 三平方の定理 30 60 90 1 2 3と1 2 3 30 60 90 働きアリ



中学生 数学 3年 三平方の定理 ピタゴラスの定理 練習問題 受験と家庭教師 掲示板 s 楽天ブログ




三平方の定理の証明と使い方




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
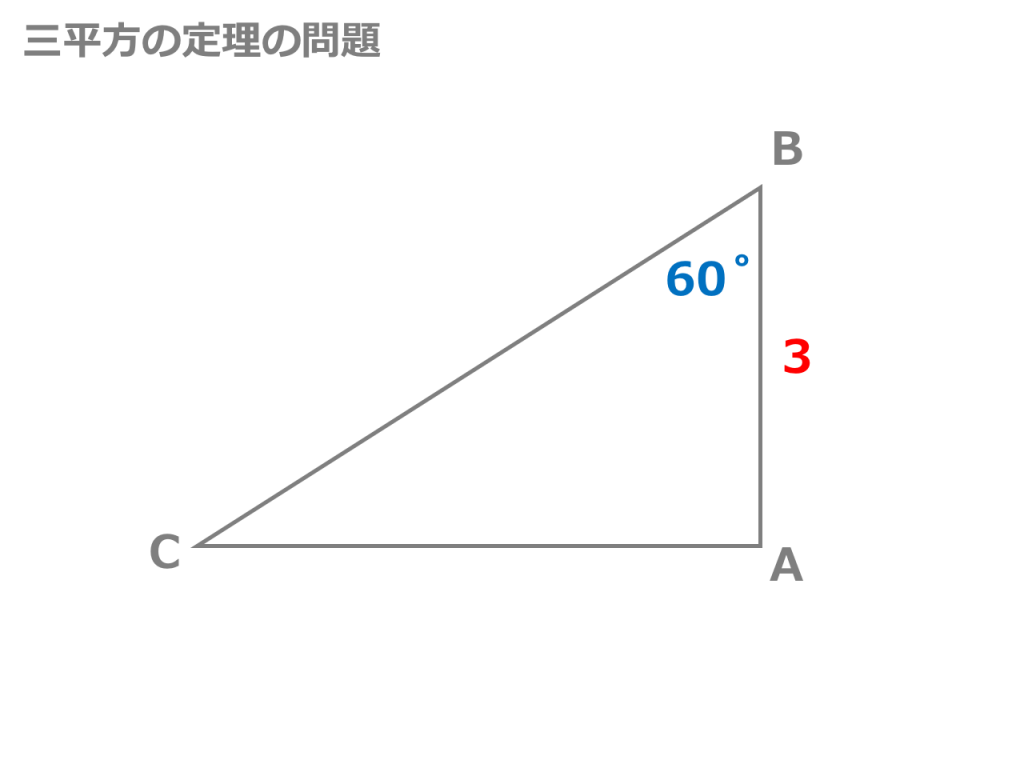



3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく
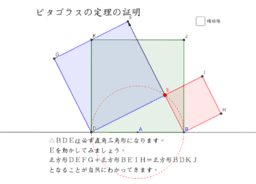



ピタゴラスの定理 三平方の定理 の証明 Geogebra
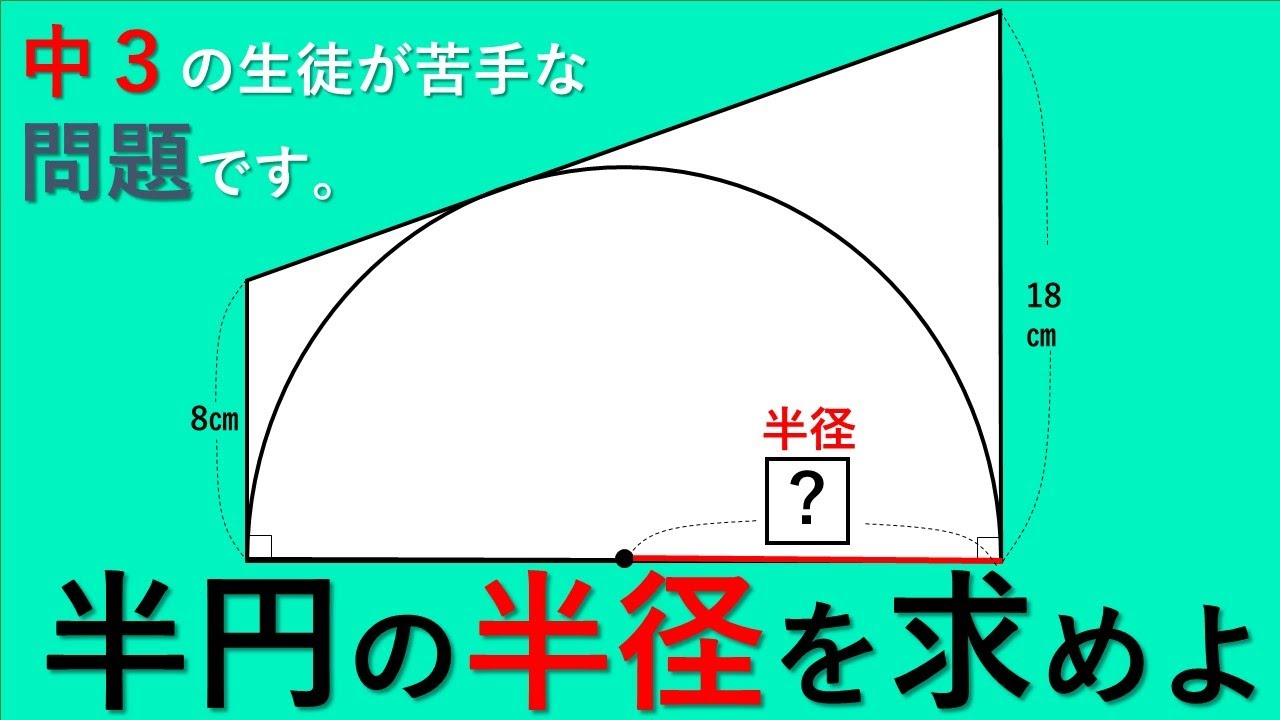



受験生の必見 三平方の定理の盲点 勉強 Youtube スタディチューブ




三平方の定理の適用 2017年度前期日程の奈良教育大学教育学部数学教育専修の入試問題 身勝手な主張



中学生 数学 3年 三平方の定理 ピタゴラスの定理 練習問題 受験と家庭教師 掲示板 s 楽天ブログ




正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




数学 中3 61 三平方の定理 基本編 Youtube




三平方の定理 無料で使える中学学習プリント



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
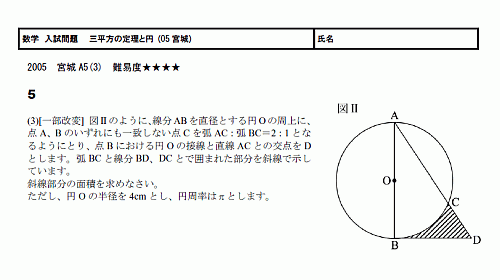



三平方の定理と円 スタディーx



1




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張




ピタゴラスの定理 Wikipedia




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




フェルマーの最終定理のn 2の場合は答えは無数にある ピタゴラス数 ちょぴん先生の数学部屋




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




三角柱の体積を求める問題です 三平方 ピタゴラスの定理の応用です 解ける方解き方 Clear




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理の練習問題10問 解き方の解説 数学fun
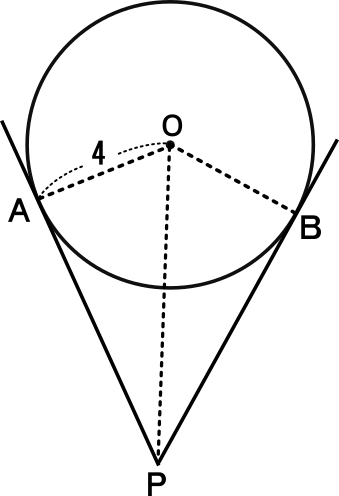



中学3年数学練習問題 三平方の定理の復習テスト
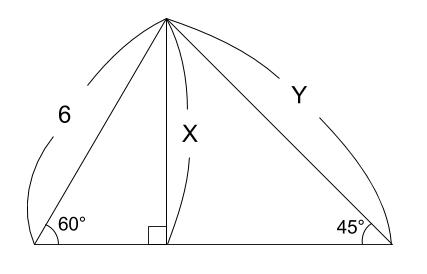



中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori




三平方の定理 ピタゴラスの定理 の例題や計算のやり方 証明 応用 難問などのまとめはこちらです 行間 ぎょうのあいだ 先生
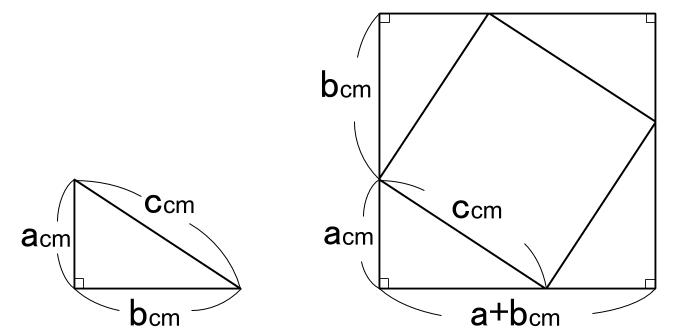



中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




Math 高校入試の難問 三平方の定理 30 60 90 1 2 3と1 2 3 30 60 90 働きアリ




中学受験算数 等積変形の利用 ヒポクラテスの月




世界一わかりやすい数学問題集中3 7章 三平方の定理




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




ピタゴラスの定理 Wikipedia




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ



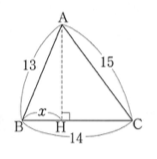
Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4



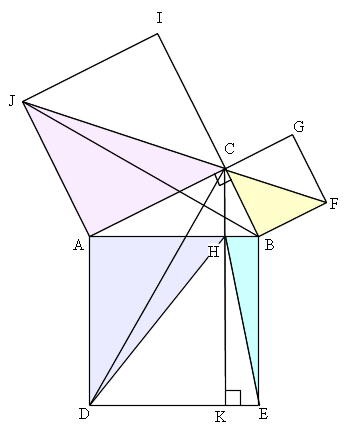
コラム ピタゴラスの定理 江戸の数学



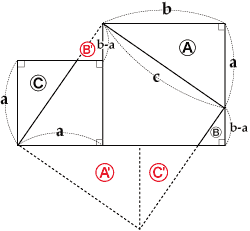
中学数学 三平方の定理




世界が変わる裏技 三平方の定理を5秒で計算するテクニック Youtube




三平方の定理 ピタゴラスの定理 の証明まとめ5選 全部でいくつあるの 遊ぶ数学



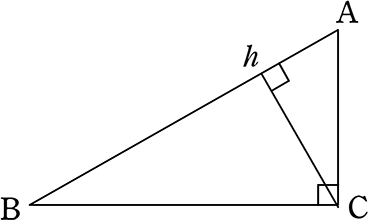
合同条件と相似条件 三平方の定理や円周角の定理は楽勝だ 数検1級合格対策




世界一わかりやすい数学問題集中3 7章 三平方の定理




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook




三平方の定理の応用
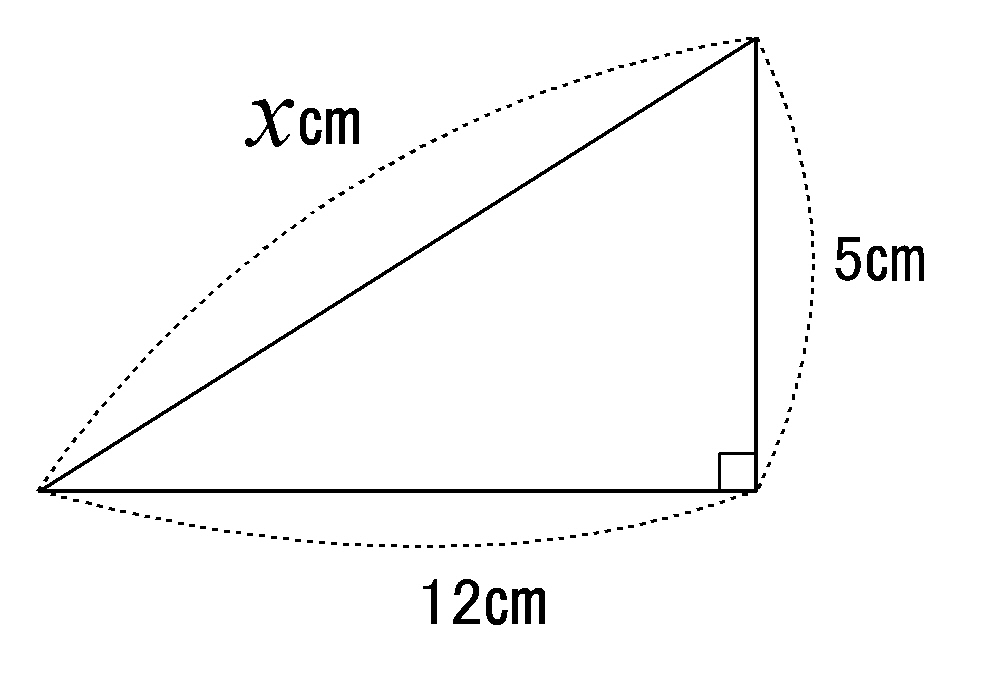



Wordで使える 三平方の定理の図 Wordで数学問題プリントを作ろう




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



1




三平方の定理 の新着タグ記事一覧 Note つくる つながる とどける




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
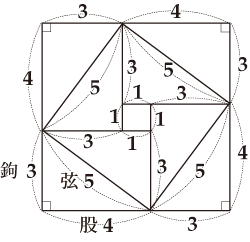



コラム ピタゴラスの定理 江戸の数学




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理の証明と使い方




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



1



1




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題



0 件のコメント:
コメントを投稿