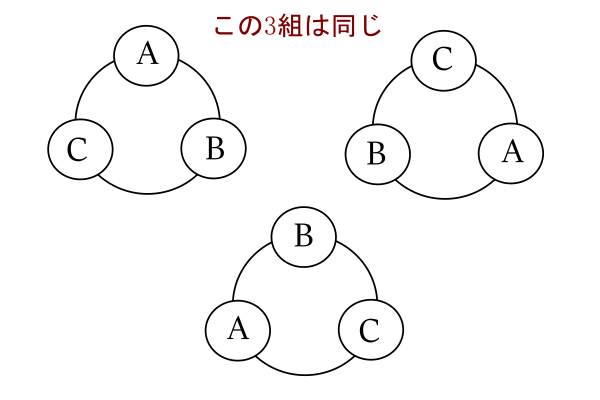
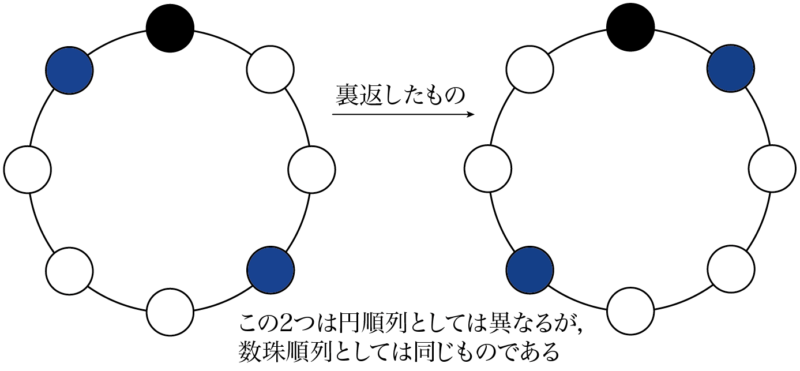
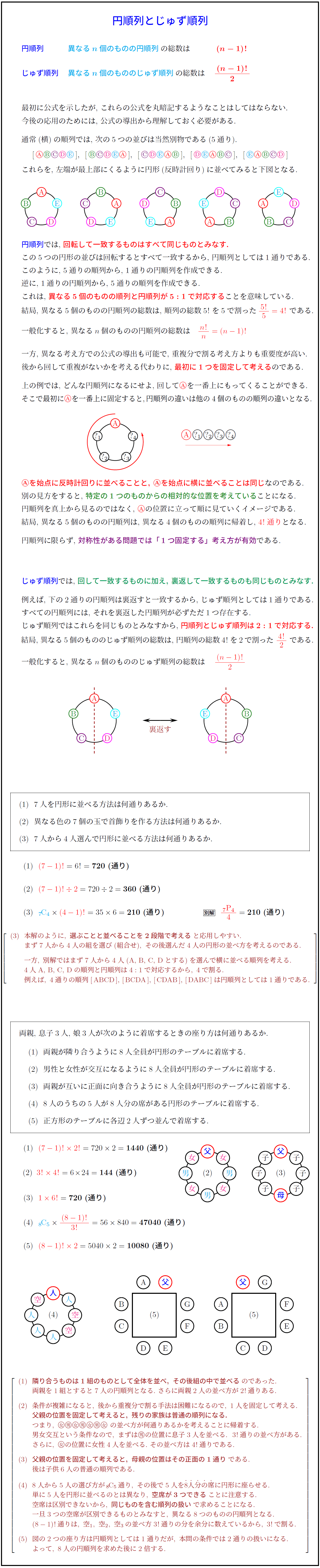
円順列とじゅず順列 4 Schoolmath S Diary
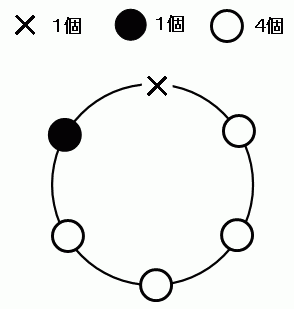
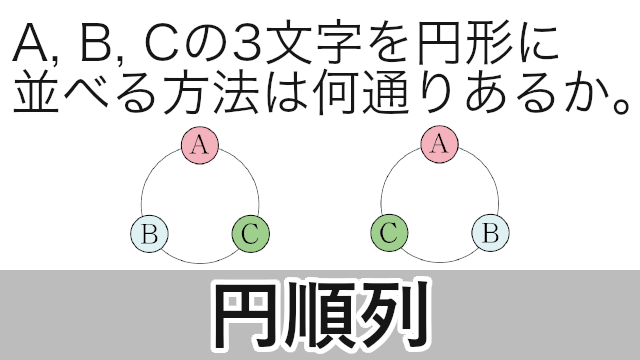
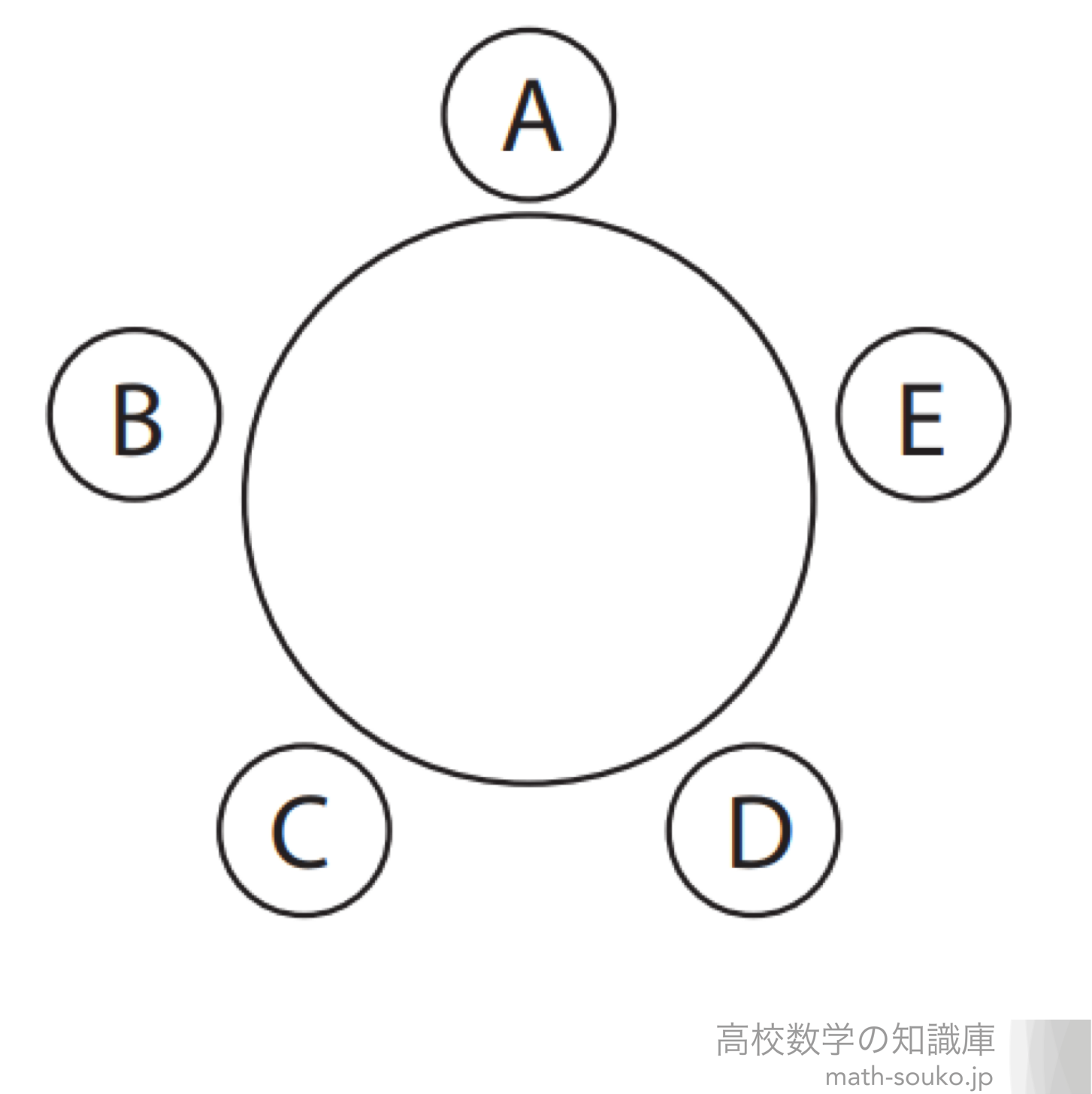
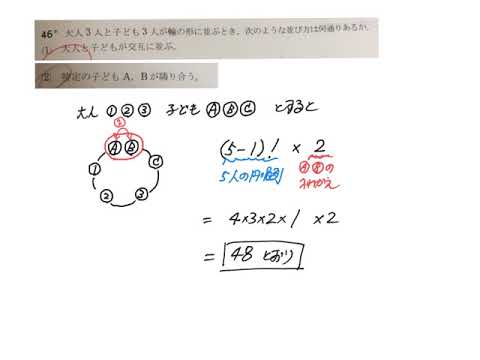
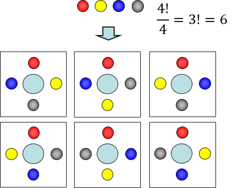
21/8/17 順列の特訓プリントです (`・ω・´) 図を描くのが解くためのカギです (*´ω`*) 数学A 順列 人を並べる特訓① 数学A 順列 桁数問題特訓① 数学A 順列 辞書式配列・小さい順特訓① 数学A 順列 円順列 (人を並べる)特訓① 数学A 順列 円順列 (図形の色塗り)特訓①/8/ 円順列とは 円順列をつかうのは何かを円形に並べるときですよね。 よく出てくるのが円形のテーブルに座る問題であったり、あとで扱いますが立方体に色を塗る問題だったりします。 公式で書くとすごいシンプルで、異なるn個の円順列の数は (n1)! で表されます。 つまり5人の子供を丸いテーブルに座らせるさい、その座らせ方は (51)! 、4! で24通り
数学 円順列
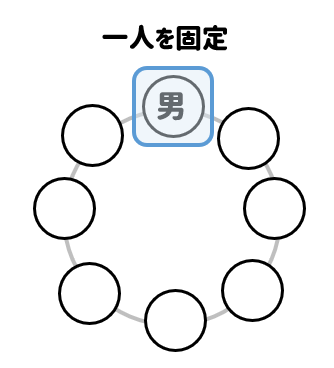
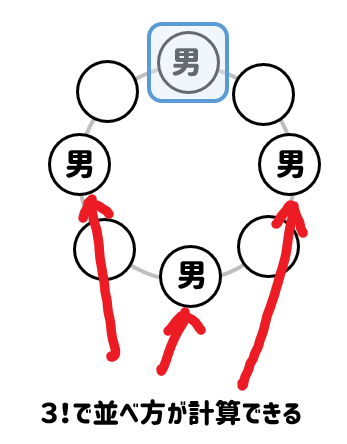
数学 円順列-13/3/17 円卓に座るというのは、 標準円形に並べる(円順列) で見た「円順列」の問題です。 回転して同じ座り方になるものを除く 必要があります。 まずは、円卓の座り方が全部で何通りあるかを考えます。 数え方はいろいろありますが、 一人を固定して 考えてみましょう。 とりあえず、A に注目しましょう。 A を基準に、他の4人がどう座るかを考えます円順列の前提条件と重要な"制限" 順列と円順列は、一列に並べているか、円形に並べているかの違いしかありません。 しかしこの、円形という並びが 場合の数を考える上で超大事なポイント になります。 では具体的にみていきましょう。
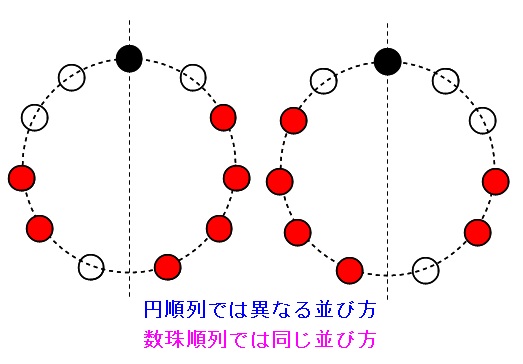
円順列と数珠順列の考え方や公式と問題の解き方
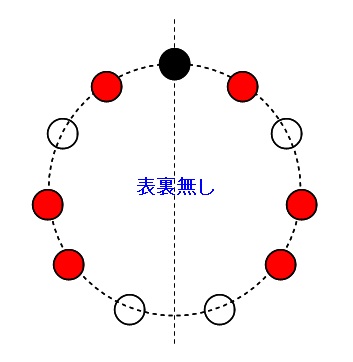
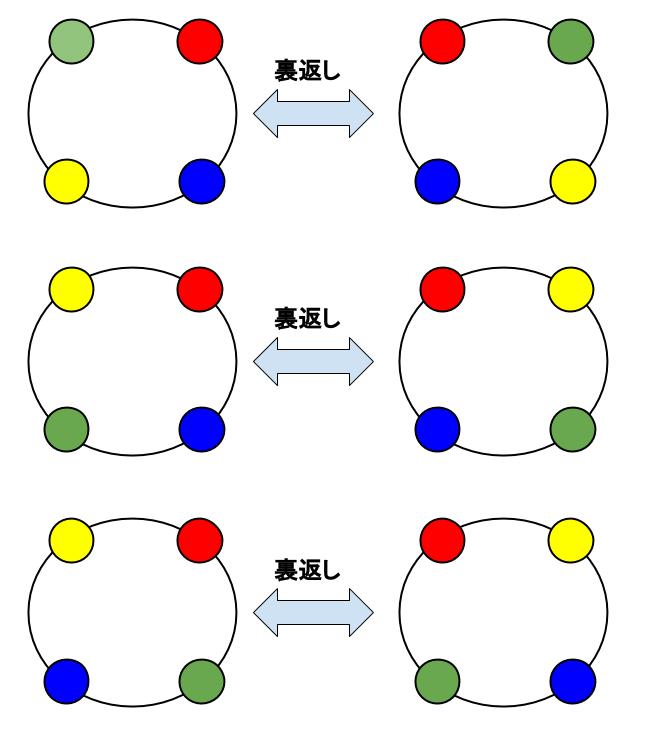
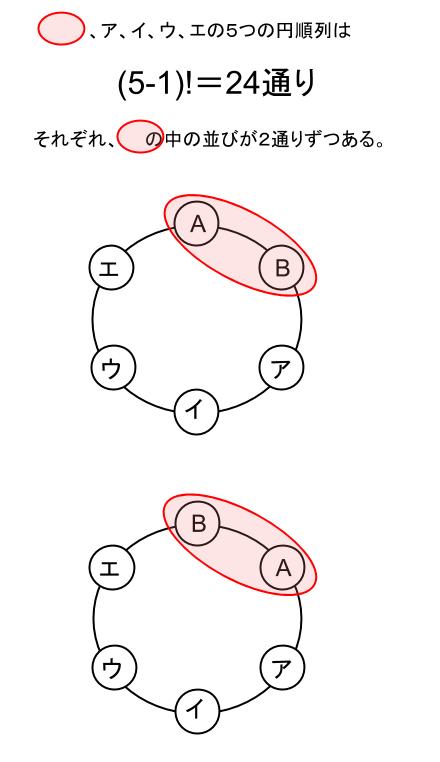
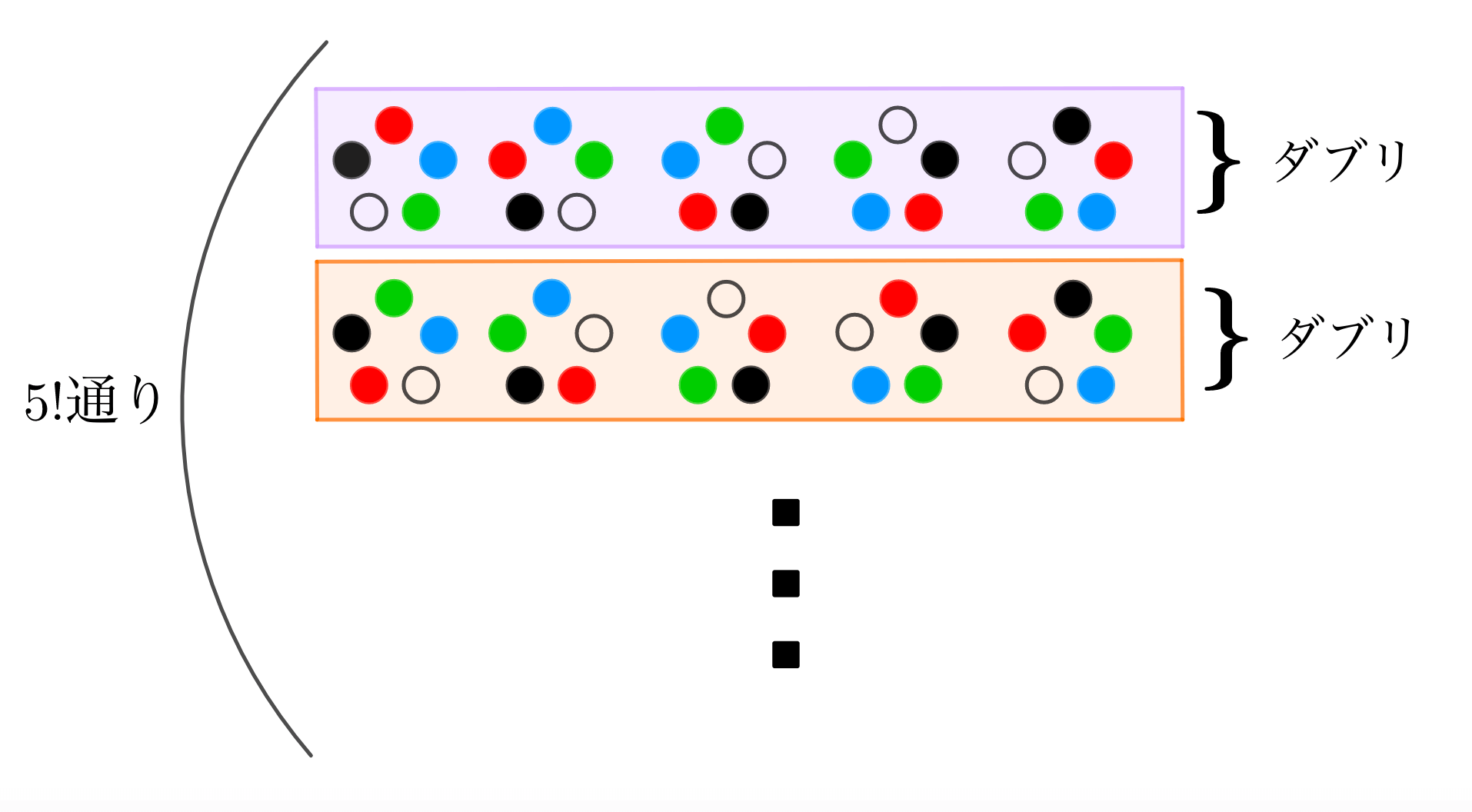
= m ×(m−1)×⋯× 2×1 を使って公式を書き換えると, m P n = m ( m − 1) ⋯ ( m − n 1) = m!18/4/ このとき x, y, z の組合せは ( x, y, z) = ( 1, 1, 4), ( 1, 2, 3), ( 2, 2, 2) の3通りになる。 考えやすいものから1つずつ確認していく。 ( 2, 2, 2) は数字の入れ替えがそもそもないため,円順列としても1通りである。 ( 1, 1, 4) に対して入れ替えを考えると,他に ( 1, 4, 1), ( 4, 1, 1) が考えられるから,次の3つの図のようになる。 3つの並べ方は異なるように見えるが,回転みんな(生活) みんな(数学) みんな(科学) みんな(実学) みんな(その他) 棒;
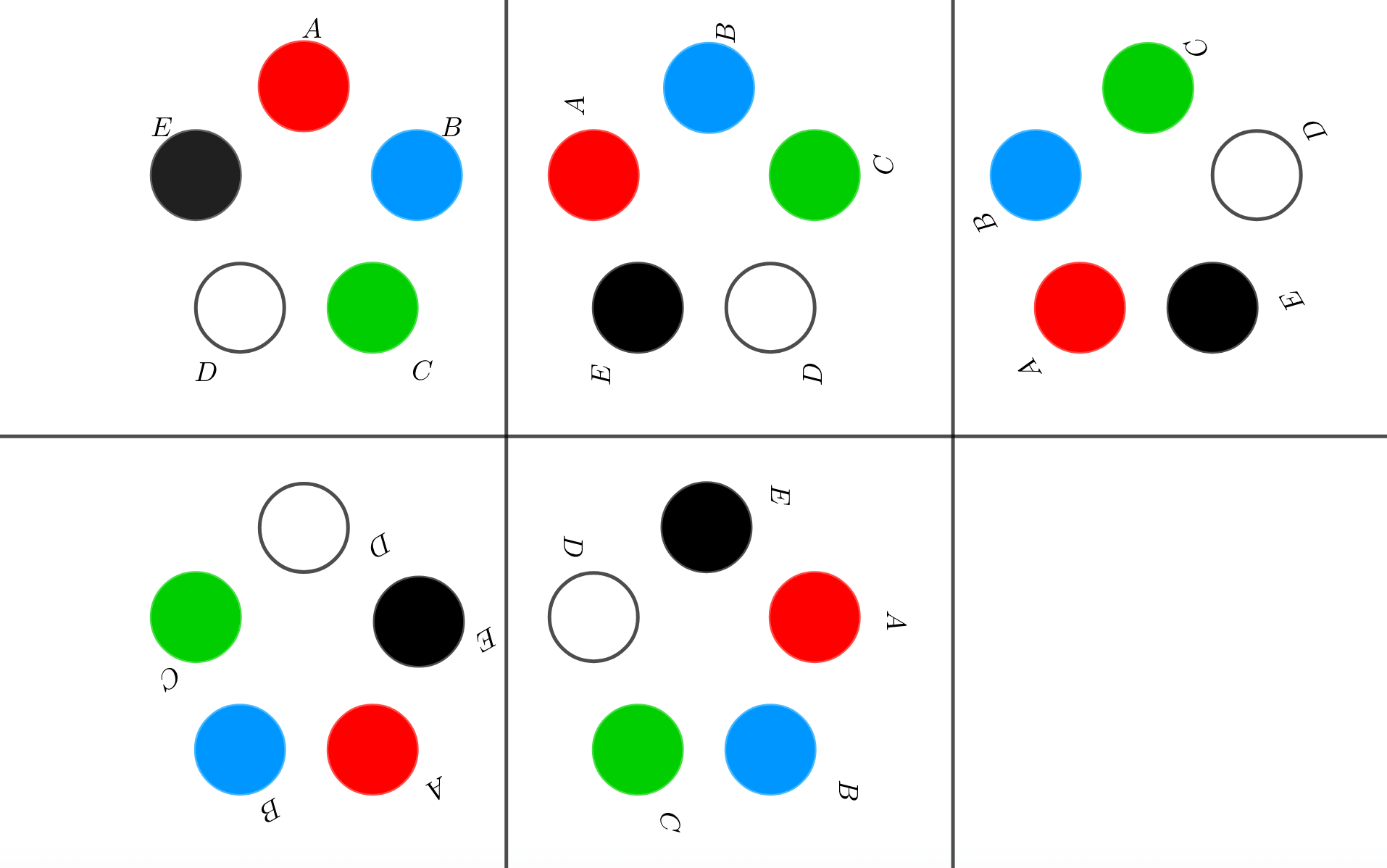
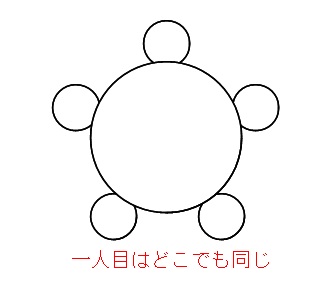
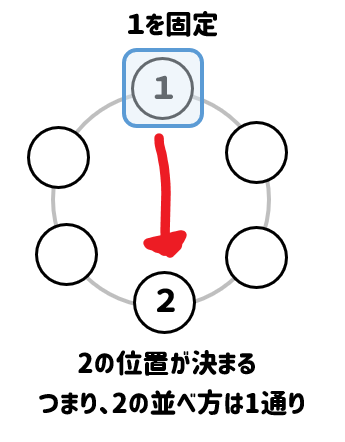
円順列の問題の解き方 何かで固定して(回転を止めて),残されたものの普通の順列の問題として考える. 異なる $n$ 個の円順列は,回転を止めるための固定に1個使うと,残りの $n1$ 個の順列になるので $(n1)!$ 通り21/7/21 円順列 とは、 いくつかの異なるものを円形に並べる順列 のことです。 たとえば、複数の人が円形のテーブルに沿って座る場合が円順列です。 一般に、 円順列の総数 は以下のように定義され高校数学Aで学習する場合の数の単元から 「平面、立体の塗り分け」 についての問題をまとめておきます。 今回の記事を通して、問題の解き方を身につけていきましょう。 取り上げる問題はこちら! 問題① 下の図のように4個の部分に区切った紙
数学 円順列のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
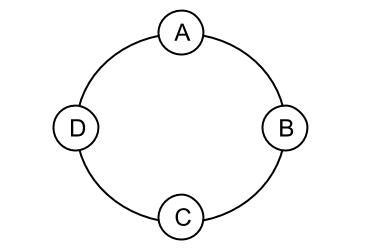
 |  |  |
 |  |  |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
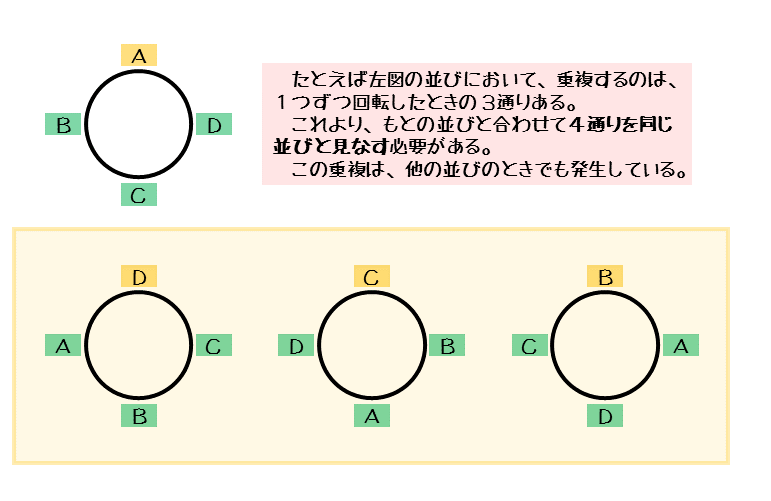
今回のテーマは 「円順列」 だよ。 これまでの順列では、例えば5人の人を「a、b、c、d、e」と1列に並べたよね。 円順列 では、これを円形に並べるんだ。 a e b d c これって、一列に並べる順列と何が違うの?と思うかも知れない。難しい重複円順列の一般的解法 重複円順列の考え方 周期解決法とコーシー・フロベニウス定理 松本睦郎(札幌啓成高等学校 講師) Episode1 難しい重複円順列 大学への数学14 年10 月号「秋の夜長に数え歌」(P12~)に次のような重複円順列の問題があっ た。





0 件のコメント:
コメントを投稿